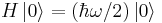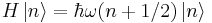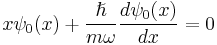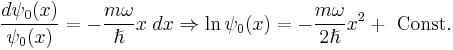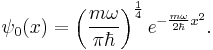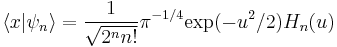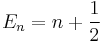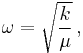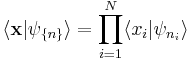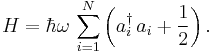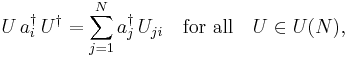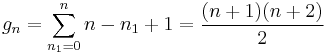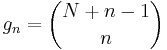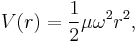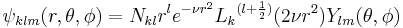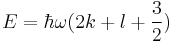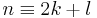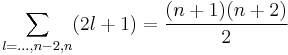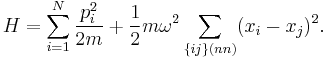Quantum harmonic oscillator
- "QHO" redirects here. It is also the IATA airport code for all airports in the Houston area.
The quantum harmonic oscillator is the quantum mechanical analog of the classical harmonic oscillator. It is one of the most important model systems in quantum mechanics because an arbitrary potential can be approximated as a harmonic potential at the vicinity of a stable equilibrium point. Furthermore, it is one of the few quantum mechanical systems for which a simple exact solution is known.
Contents |
One-dimensional harmonic oscillator
Hamiltonian and energy eigenstates


In the one-dimensional harmonic oscillator problem, a particle of mass m is subject to a potential V(x) given by
where ω is the angular frequency of the oscillator. In classical mechanics, 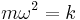 is called the spring stiffness coefficient, force constant or spring constant, and
is called the spring stiffness coefficient, force constant or spring constant, and 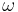 the angular frequency.
the angular frequency.
The Hamiltonian of the particle is:
where 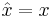 is the position operator, and
is the position operator, and 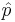 is the momentum operator, given by
is the momentum operator, given by
The first term in the Hamiltonian represents the kinetic energy of the particle, and the second term represents the potential energy in which it resides. In order to find the energy levels and the corresponding energy eigenstates, we must solve the time-independent Schrödinger equation,
We can solve the differential equation in the coordinate basis, using a spectral method. It turns out that there is a family of solutions. In the position basis they are
The functions Hn are the Hermite polynomials:
The corresponding energy levels are
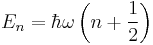 .
.
This energy spectrum is noteworthy for three reasons. Firstly, the energies are "quantized", and may only take the discrete half-integer multiples of 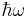 . This is a feature of many quantum mechanical systems. In the following section on ladder operators, we will engage in a more detailed examination of this phenomenon. Secondly, the lowest achievable energy is not zero, but
. This is a feature of many quantum mechanical systems. In the following section on ladder operators, we will engage in a more detailed examination of this phenomenon. Secondly, the lowest achievable energy is not zero, but 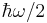 , which is called the "ground state energy" or zero-point energy. In the ground state, according to quantum mechanics, an oscillator performs null oscillations and its average kinetic energy is positive. It is not obvious that this is significant, because normally the zero of energy is not a physically meaningful quantity, only differences in energies. Nevertheless, the ground state energy has many implications, particularly in quantum gravity. The final reason is that the energy levels are equally spaced, unlike the Bohr model or the particle in a box.
, which is called the "ground state energy" or zero-point energy. In the ground state, according to quantum mechanics, an oscillator performs null oscillations and its average kinetic energy is positive. It is not obvious that this is significant, because normally the zero of energy is not a physically meaningful quantity, only differences in energies. Nevertheless, the ground state energy has many implications, particularly in quantum gravity. The final reason is that the energy levels are equally spaced, unlike the Bohr model or the particle in a box.
Note that the ground state probability density is concentrated at the origin. This means the particle spends most of its time at the bottom of the potential well, as we would expect for a state with little energy. As the energy increases, the probability density becomes concentrated at the "classical turning points", where the state's energy coincides with the potential energy. This is consistent with the classical harmonic oscillator, in which the particle spends most of its time (and is therefore most likely to be found) at the turning points, where it is the slowest. The correspondence principle is thus satisfied.
Ladder operator method
The spectral method solution, though straightforward, is rather tedious. The "ladder operator" method, due to Paul Dirac, allows us to extract the energy eigenvalues without directly solving the differential equation. Furthermore, it is readily generalizable to more complicated problems, notably in quantum field theory. Following this approach, we define the operators a and its adjoint a†
The operator a is not Hermitian since it and its adjoint a† are not equal.
The operator a and a† have properties as below:
In the Heisenberg picture, the operators have the following time dependence:
We can also define a number operator N which has the following property:
In deriving the form of a†, we have used the fact that the operators x and p, which represent observables, are Hermitian. These observable operators can be expressed as a linear combination of the ladder operators as
The x and p operators obey the following identity, known as the canonical commutation relation:
The square brackets in this equation are a commonly-used notational device, known as the commutator, defined as
![[A,B] \ \stackrel{\mathrm{def}}{=}\ AB - BA](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/711ae254c1dabae623d830a379efe9aa.png) .
.
Using the above, we can prove the identities
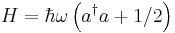
![\left[a , a^{\dagger} \right] = 1](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/c49909cd4984a38a85dc95e3349a547d.png) .
.
Now, let 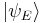 denote an energy eigenstate with energy E. The inner product of any ket with itself must be non-negative, so
denote an energy eigenstate with energy E. The inner product of any ket with itself must be non-negative, so
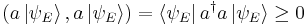 .
.
Expressing a†a in terms of the Hamiltonian:
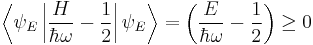 ,
,
so that E ≥ ħω/2. Note that when (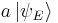 ) is the zero ket (i.e. a ket with length zero), the inequality is saturated, so that
) is the zero ket (i.e. a ket with length zero), the inequality is saturated, so that 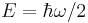 . It is straightforward to check that there exists a state satisfying this condition; it is the ground (n = 0) state given in the preceding section.
. It is straightforward to check that there exists a state satisfying this condition; it is the ground (n = 0) state given in the preceding section.
Using the above identities, we can now show that the commutation relations of a and a† with H are:
Thus, provided (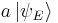 ) is not the zero ket,
) is not the zero ket,
![\begin{align}
H (a \left| \psi_E \right\rangle)
&= (\left[H,a\right] + a H) \left|\psi_E\right\rangle \\
&= (- \hbar\omega a + a E) \left|\psi_E\right\rangle \\
&= (E - \hbar\omega) (a\left|\psi_E\right\rangle)
\end{align}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/65c0753e8365603a699d9bc707bf27c3.png) .
.
Similarly, we can show that
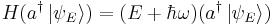 .
.
In other words, a acts on an eigenstate of energy E to produce, up to a multiplicative constant, another eigenstate of energy 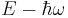 , and a† acts on an eigenstate of energy E to produce an eigenstate of energy
, and a† acts on an eigenstate of energy E to produce an eigenstate of energy 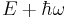 . For this reason, a is called a "lowering operator", and a† a "raising operator". The two operators together are called ladder operators. In quantum field theory, a and a† are alternatively called "annihilation" and "creation" operators because they destroy and create particles, which correspond to our quanta of energy.
. For this reason, a is called a "lowering operator", and a† a "raising operator". The two operators together are called ladder operators. In quantum field theory, a and a† are alternatively called "annihilation" and "creation" operators because they destroy and create particles, which correspond to our quanta of energy.
Given any energy eigenstate, we can act on it with the lowering operator, a, to produce another eigenstate with 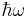 -less energy. By repeated application of the lowering operator, it seems that we can produce energy eigenstates down to E = −∞. However, this would contradict our earlier requirement that
-less energy. By repeated application of the lowering operator, it seems that we can produce energy eigenstates down to E = −∞. However, this would contradict our earlier requirement that 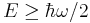 . Therefore, there must be a ground-state energy eigenstate, which we label
. Therefore, there must be a ground-state energy eigenstate, which we label 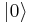 (not to be confused with the zero ket), such that
(not to be confused with the zero ket), such that
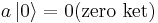 .
.
In this case, subsequent applications of the lowering operator will just produce zero kets, instead of additional energy eigenstates. Furthermore, we have shown above that
Finally, by acting on 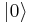 with the raising operator and multiplying by suitable normalization factors, we can produce an infinite set of energy eigenstates
with the raising operator and multiplying by suitable normalization factors, we can produce an infinite set of energy eigenstates 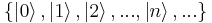 , such that
, such that
which matches the energy spectrum which we gave in the preceding section.
This method can also be used to quickly find the ground state wave function of the quantum harmonic oscillator. Indeed 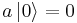 becomes
becomes
so that
After normalization this leads to the following position space representation of the ground state wave function.
Natural length and energy scales
The quantum harmonic oscillator possesses natural scales for length and energy, which can be used to simplify the problem. These can be found by nondimensionalization. The result is that if we measure energy in units of 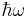 and distance in units of
and distance in units of 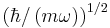 , then the Schrödinger equation becomes:
, then the Schrödinger equation becomes:
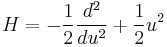 ,
,
and the energy eigenfunctions and eigenvalues become
where 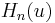 are the Hermite polynomials.
are the Hermite polynomials.
To avoid confusion, we will not adopt these natural units in this article. However, they frequently come in handy when performing calculations.
Diatomic molecules
In diatomic molecules, the natural frequency is given by
where ω = 2πf is the angular frequency, k is the force constant of the bond, and μ is the reduced mass. "Quantum Harmonic Oscillator". Hyperphysics. http://hyperphysics.phy-astr.gsu.edu/hbase/quantum/hosc.html. Retrieved 24 September 2009.
N-dimensional harmonic oscillator
The one-dimensional harmonic oscillator is readily generalizable to N dimensions, where N = 1, 2, 3, ... . In one dimension, the position of the particle was specified by a single coordinate, x. In N dimensions, this is replaced by N position coordinates, which we label x1, ..., xN. Corresponding to each position coordinate is a momentum; we label these p1, ..., pN. The canonical commutation relations between these operators are
![\begin{matrix}
\left[x_i , p_j \right] &=& i\hbar\delta_{i,j} \\
\left[x_i , x_j \right] &=& 0 \\
\left[p_i , p_j \right] &=& 0
\end{matrix}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/1a0fb98f21003d33bc6ba6cb0d3e9246.png) .
.
The Hamiltonian for this system is
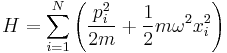 .
.
As the form of this Hamiltonian makes clear, the N-dimensional harmonic oscillator is exactly analogous to N independent one-dimensional harmonic oscillators with the same mass and spring constant. In this case, the quantities x1, ..., xN would refer to the positions of each of the N particles. This is a convenient property of the  potential, which allows the potential energy to be separated into terms depending on one coordinate each.
potential, which allows the potential energy to be separated into terms depending on one coordinate each.
This observation makes the solution straightforward. For a particular set of quantum numbers {n} the energy eigenfunctions for the N-dimensional oscillator are expressed in terms of the 1-dimensional eigenfunctions as:
In the ladder operator method, we define N sets of ladder operators,
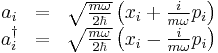 .
.
By a procedure analogous to the one-dimensional case, we can then show that each of the ai and a†i operators lower and raise the energy by ℏω respectively. The Hamiltonian is
This Hamiltonian is invariant under the dynamic symmetry group U(N) (the unitary group in N dimensions), defined by
where 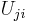 is an element in the defining matrix representation of U(N).
is an element in the defining matrix representation of U(N).
The energy levels of the system are
![E = \hbar \omega \left[(n_1 + \cdots + n_N) + {N\over 2}\right]](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/31c13fe44d74f8b03561bb74fb57419c.png) .
.
As in the one-dimensional case, the energy is quantized. The ground state energy is N times the one-dimensional energy, as we would expect using the analogy to N independent one-dimensional oscillators. There is one further difference: in the one-dimensional case, each energy level corresponds to a unique quantum state. In N-dimensions, except for the ground state, the energy levels are degenerate, meaning there are several states with the same energy.
The degeneracy can be calculated relatively easily. As an example, consider the 3-dimensional case: Define n = n1 + n2 + n3. All states with the same n will have the same energy. For a given n, we choose a particular n1. Then n2 + n3 = n − n1. There are n − n1 + 1 possible groups {n2, n3}. n2 can take on the values 0 to n − n1, and for each n2 the value of n3 is fixed. The degree of degeneracy therefore is:
Formula for general N and n [gn being the dimension of the symmetric irreducible nth power representation of the unitary group U(N)]:
The special case N = 3, given above, follows directly from this general equation.
Example: 3D isotropic harmonic oscillator
The Schrödinger equation of a spherically-symmetric three-dimensional harmonic oscillator can be solved explicitly by separation of variables, see this article for the present case. This procedure is analogous to the separation performed in the hydrogen-like atom problem, but with the spherically symmetric potential
where  is the mass of the problem. Because m will be used below for the magnetic quantum number, mass is indicated by
is the mass of the problem. Because m will be used below for the magnetic quantum number, mass is indicated by  , instead of m, as earlier in this article.
, instead of m, as earlier in this article.
The solution reads
where
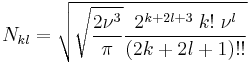 is a normalization constant.
is a normalization constant.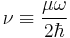
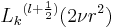 are generalized Laguerre polynomials. The order k of the polynomial is a non-negative integer.
are generalized Laguerre polynomials. The order k of the polynomial is a non-negative integer.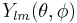 is a spherical harmonic function.
is a spherical harmonic function. is the reduced Planck constant:
is the reduced Planck constant: 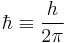 .
.
The energy eigenvalue is
The energy is usually described by the single quantum number
Because k is a non-negative integer, for every even n we have 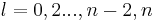 and for every odd n we have
and for every odd n we have 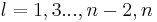 . The magnetic quantum number m is an integer satisfying
. The magnetic quantum number m is an integer satisfying 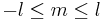 , so for every n and l there are 2l+1 different quantum states, labeled by m. Thus, the degeneracy at level n is
, so for every n and l there are 2l+1 different quantum states, labeled by m. Thus, the degeneracy at level n is
where the sum starts from 0 or 1, according to whether n is even or odd. This result is in accordance with the dimension formula above.
Coupled harmonic oscillators
In this problem, we consider N equal masses which are connected to their neighbors by springs, in the limit of large N. The masses form a linear chain in one dimension, or a regular lattice in two or three dimensions.
As in the previous section, we denote the positions of the masses by x1, x2, ..., as measured from their equilibrium positions (i.e. xk = 0 if particle k is at its equilibrium position.) In two or more dimensions, the xs are vector quantities. The Hamiltonian of the total system is
The potential energy is summed over "nearest-neighbor" pairs, so there is one term for each spring.
Remarkably, there exists a coordinate transformation to turn this problem into a set of independent harmonic oscillators, each of which corresponds to a particular collective distortion of the lattice. These distortions display some particle-like properties, and are called phonons. Phonons occur in the ionic lattices of many solids, and are extremely important for understanding many of the phenomena studied in solid state physics.
See also
- Gas in a harmonic trap
- Creation and annihilation operators
- Coherent state
- Morse potential
- Hooke's atom
- Bertrand's theorem
References
- Griffiths, David J. (2004). Introduction to Quantum Mechanics (2nd ed.). Prentice Hall. ISBN 0-13-805326-X.
- Liboff, Richard L. (2002). Introductory Quantum Mechanics. Addison-Wesley. ISBN 0-8053-8714-5.
External links
- Quantum Harmonic Oscillator
- Calculation using a noncommutative free monoid: (mathematical version) / (abbreviated version)
- Rationale for choosing the ladder operators
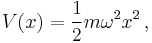
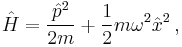
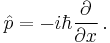
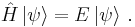
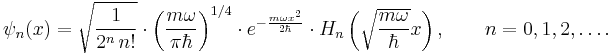
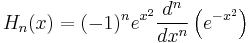
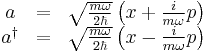
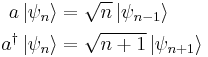
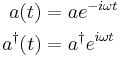
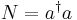

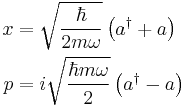
![[x,p] = i\hbar \, .](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/9c014e19035c93fae5850a04f484b0f7.png)
![\begin{align}
\left[ H, a \right] &= - \hbar \omega a \\
\left[ H, a^\dagger \right] &= \hbar \omega a^\dagger \, .
\end{align}](/2010-wikipedia_en_wp1-0.8_orig_2010-12/I/fcfaf0b200e5c524b9ad8b5410067b1e.png)